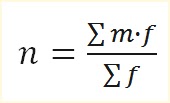PRAKTIKUM STATISTIK RADIASI LATAR

PRAKTIKUM STATISTIK RADIASI LATAR

( mengetahui frekuensi cacah latar yang terjadi , ketika jumlah cacah dalam 10 detik  diukur 100 kali)

             

Pengukuran intensitas radiasi yang dilakukan secara berulang pasti akan memperoleh hasil pengukuran yang berbeda-beda. Sehingga dalam pengukuran intensitas radiasi harus dilakukan secara berulang, baik beberapa kali atau dalam selang waktu cukup panjang, yang berarti akumulasi nilai dari pengulangan waktu beberapa detik. Nilai ukur sebenarnya diduga berada di dalam rentang nilai rata-rata ± nilai simpangannya.


Sebagaimana perhitungan matematika biasa, nilai rata-rata dapat dihitung

dengan persamaan berikut :

Sifat acak suatu pengukuran selalu mengikuti suatu distribusi tertentu, sebagai contoh eksperimen uang logam dan dadu di atas mengikuti distribusi binomial. Bila distribusi binomial tersebut mempunyai probabilitas sangat kecil maka akan berubah menjadi distribusi Poisson. Oleh karena aktivitas zat radioaktif bersifat acak maka intensitas radiasi yang terukurpun akan bersifat acak sehingga data hasil pengukurannya juga akan mengikuti distribusi Gauss atau poisson.

Distribusi poisson adalah

• Distribusi nilai-nilai bagi suatu variabel random X (X diskret), yaitu banyaknya hasil percobaan yang terjadi dalam suatu interval waktu tertentu atau di suatu daerah tertentu.
• Distribusi probabilitas diskret yang menyatakan peluang jumlah peristiwa yang terjadi pada periode waktu tertentu apabila rata-rata kejadian tersebut diketahui dan dalam waktu yang saling bebas sejak kejadian terakhir.
• Probabilitas lebih dari satu hasil percobaan yang terjadi dalam interval waktu yang singkat atau dalam daerah yang kecil dapat diabaikan. Selain itu, Distribusi poisson banyak digunakan dalam hal berikut:
• Rumus Pendekatan Peluang Poisson untuk Binomial

Apabila nilai harapan kejadian pada suatu interval adalah n, maka probabilitas terjadi peristiwa sebanyak m kali (m adalah bilangan bulat non negatif, k = 0, 1, 2, ...) maka sama dengan

 

dimana

  e adalah basis logaritma natural (e = 2.71828...)

m adalah jumlah kejadian suatu peristiwa  — peluang yang diberikan oleh fungsi ini

m! adalah faktorial dari m

n adalah bilangan riil positif, sama dengan nilai harapan peristiwa yang terjadi dalam interval tertentu.  jadi untuk nilai n yang memiliki frekuensi tertentu dapat dituliskan

 

Dimana f adalah frekuensi dari m. sedangkan m disini  adalah cacah latar yang terjadi dalam selang waktu tertentu.

Grafik sebaran distribusi poisson :

Perbandingan distribusi Poisson (titik hitam) dengan distribusi binomial dengan n = 10 (garis merah), n = 20 (garis biru), n = 1000 (hijau line). Semua distro memiliki rata-rata 5. Sumbu horizontal menunjukkan jumlah k acara. Perhatikan bahwa ketika n semakin besar, distribusi Poisson menjadi perkiraan semakin lebih baik untuk distribusi binomial dengan mean yang sama.

Ralat Statistik dalam perhitungan nilai cacah radiasi

Rating: 4.5




Ralat Statistik dalam perhitungan nilai cacah radiasi

 (Fisika dan sains kali ini akan berbagi ilmu dalam menghitung nilai cacah untuk pengukuran berulang yang bervariasi dan menghitung deviasi persentase sebuah pengukuran tunggal dari nilai rata-rata)


Ralat/ Ketidakpastian
Pengetahuan yang kita miliki tentang dunia fisika sebagian besar diperoleh dengan melakukan percobaan dan melakukan pengukuran. Jadi adalah suatu hal yang penting untuk memahami bagaimana untuk mengungkapkan data dan bagaimana menganalisis dan menarik kesimpulan yang berarti dari itu.


Dalam melakukan hal ini (mengungkapkan data dan menganalisis) sangat penting untuk memahami bahwa semua pengukuran besaran fisika tunduk pada ketidakpastian. Tidak pernah mungkin untuk mengukur sesuatu dengan tepat tanpa ralat. Untuk membuat kesalahan sekecil mungkin dapat diupayakan tetapi tatap selalu ada ketidakpastian.

  Ketidak-pastian sebenarnya tidak hanya berasal dari pengukuran saja melainkan berasal dari semua langkah analisis mulai dari preparasi sampel,faktor kesalahan alat, kesalahan  personil, kesalahan metode, dan pengukurannya sendiri. Akan tetapi dalam pembahasan ini hanya akan dipelajari ketidak-pastian  yang berasal dari proses pengukuran dan faktor yang berkaitan langsung dengan pengukuran. Setiap pengukuran selalu mempunyai kesalahan (eror) oleh karena itu hasil pengukuran atau kalkulasi yang berdasarkan hasil pengukuran harus ditampilkan dalam bentuk suatu rentang nilai (bukan nilai tunggal). Rentang nilai tersebut adalah ketidak-pastian  suatu pengukuran. Nilai ukur sebenar-nya  diduga berada di dalam rentang nilai tersebut. Pertanyaannya adalah “seberapa yakinkah nilai ukur sebenarnya berada di dalam rentang nilai

tersebut”. 

Hasil pengukuran disajikan dengan “format” seperti berikut ini. 

λ adalah suatu faktor yang menunjukkan tingkat kepercayaan (level of confidence) dengan nilai sebagaimana tabel berikut.

 beberapa jenis tingkat kepercayaan yang sering digunakan. 

nilai dugaan sebenarnya ditunjukan di dalam rentang nilai yang ditamplkan debgab tingkat kepercayaan 1 sigma ( gambar kiri) dan 2 sigma (gambar kanan).

Memang dengan memilih tingkat kepercayaan yang semakin besar, misalnya 3 sigma, akan memperoleh kemungkinan nilai ukur sebenarnya berada di dalam rentang dugaan semakin besar, tetapi nilai rentangnya juga semakin lebar. Oleh karena itu, nilai simpangan (  σ ) harus diusahakan sekecil  mungkin, yaitu dengan cara mengulang pengukuran semakin sering atau memperpanjang waktu pengukuran.

Statistik Peluruhan Radioaktif

Jika kita mengulangi satu jenis pengamnatan secara berulang. maka hasilnya sering li (iduk sumu. tetapi berkisar padu scbuuh nilai rata-rutu tertentu. Lcburnya hasi distrihusi tersebut ditandai dengan adanya deviasi standar. Dalam hal peluruhan radioaktif, jumlah partikel yang dihasilkan dan sebuah sumber stiap satuan waktu ratar rata (N strip atas) dapat dijelaskun dengan sebuuh distribusi yang disebut distribusi Poisson. Distribusi ini cukup baik untuk sederetan peristiwa yang sungguh-sungguh acak. Deviasi standar dan nilai cacah rala-rala ini dirumuskan: 

deviasi standart radiasi

dimana 

N rata-rata

 deviasi standart ini juga dapat dinyatakan dalam persen yaitu dengan persamaan:

Efek Jarak sumber radiasi pada counter berjendela tipis terhadap nilai cacah

Rating: 3.5

Praktikum Efek Jarak sumber radiasi pada counter Berjendela Tipis Terhadap Nilai cacah

A.    Tujuan Percobaan

1.      menyelidiki pengaruh jarak antara sumber radiasi dan counter berjendela tipis terhadap nilai cacah radiasi sumber radioaktif 

Dasar teori

Sistem  pencacah   radiasi   yang   digunakan   dalam  aplikasi   dan   penelitian  nuklir,  bertujuan untuk mengukur  kuantitas dan energi   radiasi.  Kuantitas  radiasi   merupakan   jumlah   radiasi   yang   memasuki   detektor.   Besarnya  kuantitas radiasi ini dipengaruhi oleh beberapa faktor, antara lain: aktivitas  sumber   radiasi,   jenis   dan   energi   radiasi,   serta   jarak   dan   jenis   penahan  radiasi  yang disimpan di  antara sumber   radiasi  dan detektor.  Sedangkan  energi   radiasi  merupakan kekuatan dari   setiap  radiasi  yang dipancarkan  oleh  suatu  sumber   radiasi.  Besarnya   energi   radiasi   ini  bergantung pada  jenis radionuklidanya. Jenis radionuklida yang berbeda akan memancarkan  radiasi dengan energi yang berbeda.